辐射过程
辐射过程·
部分内容待补充
辐射是我们认识天体的手段
黑体辐射·
- 大气辐射窗口
一般的电磁辐射会被大气吸收,只有三个频段才能穿透。波长极短的电离辐射也可透过大气。
- 光学窗口
~300nm 到 ~900nm
- 红外窗口
若干μm波长的窄波段组成
- 射电窗口
~1mm 到 ~30m (~10MHz 到 ~300GHz)
- 光学窗口
- 热辐射
处于热平衡物体发射的辐射。
mc2 < ~kT的粒子。m=0的光子是其主要成分。
- kirchhoff定律
$\psi_e (v,T)=\alpha(v,T)\cdot B(v,T)$
- 黑体辐射
α(v,T)=1时的热辐射。
- planck公式(能量密度)
$\rho_v(T)=\frac{ 8\pi hv^3 }{ c^3 } \frac{ 1 }{ e^ \frac{ hv }{ kT } -1 }$
- stefan-boltzmann公式(辐射通量)
$B(T)=\frac{ c }{ 4 }\int_0^ { + \infty }\rho_v(T)dv = \sigma T^4$
- wien位移定律
$\lambda_{max}T = 0.29cm K$
- 辐射场状态方程
$P(T)=\frac{ \rho(T) }{ 3 }$
- planck公式(能量密度)
- kirchhoff定律
非热辐射·
未处于热平衡物体发射的辐射,如磁场环境下非热高能电子辐射。
- 电子的辐射类型
电子状态不同,辐射类型也不同。
- 回旋辐射$e(\beta\ll 1)\oplus B$
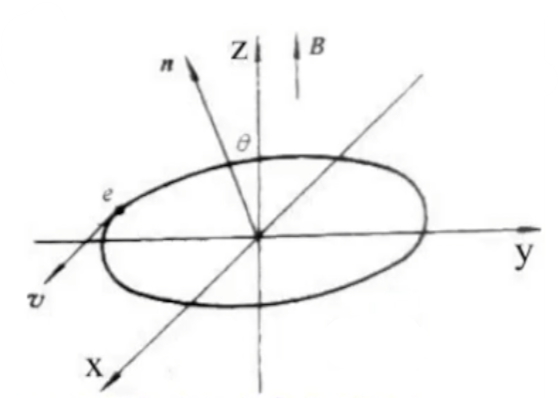
$r_L = \frac{ mcv }{ eB }$ $\omega _L = \frac{ eB }{ mc } $
单色、辐射几乎各向同性、椭圆偏振
- 同步辐射$e(\gamma\gg 1)\oplus B$
$r_0 = \gamma r_L$ $\omega _0 = \frac{ \omega _L }{ \gamma }$
辐射场为锥体
- 曲率辐射
landau能级
$\Delta E = \frac{ \hbar eB }{ mc }$ $mc^2 = \frac{ \hbar eB_q }{ mc }$
$\frac{ B }{ B_q } = \frac{ \Delta E }{ mc^2 }$
- 回旋辐射$e(\beta\ll 1)\oplus B$
- compton过程
电子与光子碰撞过程。
- compton散射
电子动能<<光子能量 时
- 逆compton散射ICS (comton辐射)
电子动能>>光子能量 时 产生 高能光子
- 设在Σ参照系中,有频率ν,与x轴夹角为θ的光子;则在Σ’(γ)系中有 $\nu’ = \gamma\nu (1-\beta cos\theta) , tan\theta’ = \frac{ sin\theta }{ \gamma(cos\theta -\beta) } $
于是在γ>>1时,有ν’~γν,tanθ’趋于0-
在讨论极端相对论粒子辐射时,一般做两次洛伦兹变换,便有ν’~γ2ν,沿电子方向。可见,逆compton散射是高能辐射的有效机制。 - Thomson散射
能量<511keV被几乎静止的电子散射
- Eddington光度
当作用于物体的引力与辐射压平衡时,星体的光度。
- 星体单位面积因吸积释放的能量:$\frac{ \frac{ GM\dot{ M } }{ R } }{ 4\pi R^2 } = \rho c = \sigma T^4$
- 吸积物中电子所受辐射压 $f_r = \frac{ \rho c\sigma_T }{ h\nu } \cdot \frac{ h\nu }{ c }$ (ρ为能量密度)
- 吸积物中质子所受引力 $f_g = \frac{ GMm_p }{ R^2 }$
- $\dot{ M }_{ Edd } = \frac{ 4\pi m_pcR }{ \sigma_T }$
- $L_{ Edd } = \frac{ GM\dot{ M }_{ Edd } }{ R } = \frac{ 4\pi m_pcGM }{ \sigma_T }$
- ~ $10^{38}( \frac{ M }{ M_{ sun } } ) erg/s$
- 星体单位面积因吸积释放的能量:$\frac{ \frac{ GM\dot{ M } }{ R } }{ 4\pi R^2 } = \rho c = \sigma T^4$
- compton散射
- 轫致辐射
自由运动电子受离子库仑场作用做加速产生的辐射。是等离子体冷却的主要因素。
- 有速度为v的电子,在正电荷数Z,数密度Nz的离子背景上运动,产生轫致辐射功率 $P \approx \frac{ 16 }{ 411 } N_{ z } Z^{ 2 } r_e^2 mc^2v$
- cherenkov辐射
源于运动电荷激发介质粒子产生电磁振荡的集体效应
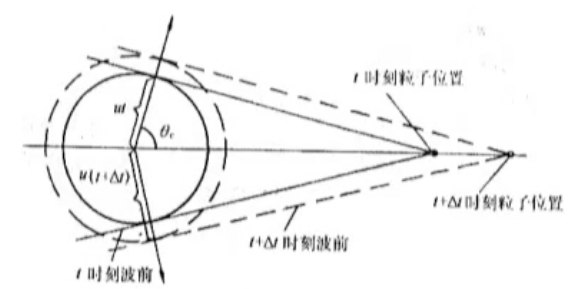
- 要求电荷速度大于介质光速(c/n),方向 $\theta _c(\omega) = arccos\frac{ 1 }{ \frac{ v }{ c }n }$
- 电磁级联($\gamma \rightarrow e^\pm$) 强子级联 $\begin{cases} \pi ^+ \rightarrow \mu ^+ + \nu _\mu \\ \pi ^- \rightarrow \mu ^- + \bar{\nu} _\mu \\ \pi ^0 \rightarrow 2\gamma \end{cases}$
