酶

发表于 2024-03-28 分类于生物化学阅读次数：本文字数： 6.6k

酶·

酶通论·

酶的概念·

酶是具有催化活性的蛋白质/核酸，也叫生物催化剂。
酶促反应是酶催化的反应;其中发生化学变化的物质叫底物。

酶催化的特点

不参与反应，不改变反应的平衡常数
酶降低活化能，加速反应速率
酶易失活
催化效率很高
高度专一性
酶的活力可控
- 酶浓度（诱导/抑制酶合成;调节酶降解）
- 激素调节酶活性
- 反馈抑制调节酶活性
- 抑制剂和激活剂调节
- 共价修饰调节
- 别构调节
- 酶原激活
- 同功酶

酶的化学组成

单纯蛋白质酶类
结合蛋白质酶类
- 酶蛋白
- 辅助因子（金属离子、金属有机物、小分子有机物）
  - 辅酶（辅酶I,II）非共价键结合
  - 辅基（FAD、FMN）共价键结合

酶的分子特点

单体酶（溶菌酶）
寡居酶（乳酸脱氢酶）
多酶复合体（丙酮酸脱氢酶系）

酶的分类·

习惯名称
- 根据底物
- 根据催化反应性质
系统名称

标明底物（两个以上用冒号隔开）及催化反应性质等

酶的六大类
1. 氧化还原类
  
  包括脱氢酶、氧化酶、过氧化物酶等
  $\ce{2A·2H + O_2 <=>[酶] 2A + 2H_2O}$
  $\ce{A·2H + O_2 <=>[酶] A + H_2O_2}$
  例：邻二苯酚的氧化反应
  
  $\ce{A·2H + B <=>[酶] A + B·2H}$
  例：乳酸脱氢酶
2. 转移酶类
  
  $\ce{A-R + B <=>[酶] A + B-R}$
  例：谷丙转氨酶
3. 水解酶类
  
  $\ce{AB + H_2O <=>[酶] AOH + BH}$
4. 裂合酶类
  
  $\ce{AB <=>[酶] A + B}$
5. 异构酶类
  
  $\ce{A <=>[酶] B}$
6. 连接酶类
  - $\ce{A + B + ATP ->[酶] AB + ADP + Pi}$
  - $\ce{A + B + ATP ->[酶] AB + AMP + PPi}$

酶的专一性·

结构专一性

底物对酶的化学结构有要求，分为绝对专一性和相对专一性。
立体专一性

在结构专一性的基础上对立体异构有要求，可分旋光异构专一性和几何异构专一性。

为什么专一
- 锁钥假说 1894年 Fischer 不完全正确
- 诱导锲合假说 1958年 Koshland
  
  酶与底物结合后，酶的构象发生变化，使得酶与底物更好的结合，从而促进反应的进行。

酶的活力测定与分离提纯·

酶活力
在一定条件下所催化的某一反应的速率（即单位时间/体积中底物减少或增加的量）
- 酶活力的测定 测定完成一定反应的时间
  测定单位时间的反应量
  办法
  - 分光光度法
    
    要求产物底物对目标光吸收率不同
    优点：简单、快速、准确、方便监测。
  - 荧光法
    
    要求产物底物具有荧光性质
    优点：灵敏度高。
    缺点：易被干扰。
  - 同位素标记法
    
    灵敏度最高。
  - 电化学法
    
    pH计、氧电极法等。
酶单位

一定条件下在一定时间内将一定量底物转化为产物的酶的量
单位：IU Kat
1IU = 1μmol/min (μ = 10^-6)
1Kat = 1mol/s
比活力

每单位质量酶所具有的活力单位数
单位：IU/mg 等

提纯

总活力损失，比活力提高。

特殊酶·

参见p4

核酶

rna酶
抗体酶

在抗体可变区有酶属性的具有催化活性的免疫球蛋白

酶促反应动力学·

研究酶促反应速率及影响其的因素

酶与底物的中间络合物学说

现象
- 一级反应特征低浓度的时候成正比
- 混合反应特征中浓度的时候成不正比部分比例增加
- 零级反应特征高浓度的时候达V_max
猜想
- 酶首先和底物结合形成ES，然后再解离成P和S
- $\ce{ S + E <=> ES -> P + S}$
验证
- 电镜直接观察到了ES

米氏方程·

$V = \frac{V_{max} \cdot [S]}{K_m + [S]}$

Meichele-Menten 提出：
$\ce{S + E <=>[K_1][K_2] SE ->[K_3] P + E }$ （其中K₁ >> K₂ / K₃）
推导出：
$\ce{V = V_{max} \frac{[S]}{K_s + [S]}}$

Briggs-Haldane 提出稳态理论：
$\ce{S + E <=>[K_1][K_2] SE <=>[K_3][K_4] P + E }$
推倒：

ES浓度变化速度：$\frac{d[ES]}{dt}$

在反应初期，
- K₄ ～ 0，
  此时 $\frac{d[ES]}{dt}$ 为 $ K_1 ( [E] - [ES] ) \cdot [S]$
- 此时 $-\frac{d[ES]}{dt}$ 为 $ K_2 \cdot [ES] + K_3 \cdot[ES] \textcircled{2}$

在稳态下：
- $ K_1 ( [E] - [ES] ) \cdot [S] = K_2 \cdot [ES] + K_3 \cdot[ES] $

即：
- $\frac{k_2 + k_3}{k_1} = \frac{( [E] - [ES] ) \cdot [S]}{[ES]} \textcircled{3} , $
- 令：$K_m = \frac{k_2 + k_3}{k_1}$
- 可得：$[ES] = \frac{[E] \cdot [S]}{K_m + [S]}\textcircled{4}$

又：
- V = K₃ [ES]，
- 可得：$V = K_3 \cdot \frac{[E] \cdot [S]}{K_m + [S]}$

当：
- [S] >> [E] 时，有 [E] = [ES]，
- 那么 $V_{max} = K_3 \cdot [E]\textcircled{7}$

此时有：
- $V = \frac{V_{max} \cdot [S]}{K_m + [S]}$（米氏方程）

所以：
- K_m >> [S] 时，V = $\frac{V_{max} \cdot [S]}{K_m}$
- K_m << [S] 时，V = V_max
- K_m = [S] 时，V = $\frac{V_{max}}{2}$
- 我们称K_m为米氏常数（mol/L）
$\textcircled{2}$ 可以判定酶的专一性和天然底物
$\textcircled{3}$ 可以计算V_max和V间的关系
$\textcircled{7}$ 可以判定反应方向与途径

注意：
- $K_m \neq K_s$，仅在 K₁ >> K₃ / K₂ 时才可近似看作 K_s，此时 $\frac{1}{K_m}$ 近似表示酶与底物的亲和力。
- $K_{max}$ 在特定的反应中是常数
- [S]很大时，$V_{max} = K_3[E]$，在这里 $K_3$（一级转换常数）即为K_cat / TN。

作图：
- 双倒数 $\frac{1}{v} = \frac{K_m}{V_{max}} \cdot \frac{1}{[S]} + \frac{1}{V_{max}}$
- Eadie-Hofstee法 $V = -K_m \cdot \frac{V}{[S]} + V_{max}$
- Hanes-Woolf法 $\frac{[S]}{V} = \frac{K_m}{V_{max}} + \frac{[S]}{V_{max}}$
- 直接作图 $V_{max} = V + \frac{V}{K_m \cdot [S]}$

多底物反应的酶促反应动力学·

双底物反应
- 单置换反应（序列反应）
  - 有序反应
    - $\ce{E + \overset{\text{领先底物}}{A} + B <=> E\overset{\text{优先结合}}{A}B <=> EPQ <=> E + \overset{\text{优先释放}}{P} + Q}$
  - 随机反应随便反应了
- 双置换反应（乒乓反应）
  
  E 与领先底物A 先反应产出 E^MOD 与 P，
  E^MOD 与底物B 再反应产出 E 与 Q，

酶的抑制作用·

指酶的必需基团变性，酶的活性下降，但不引起酶变性。

抑制程度的表示
- 相对活力分数 $a = \frac{v_1}{v_0}$
- 相对活力百分数 a%
- 抑制分数 1 - a
- 抑制百分数 (1 - a)%

抑制剂

抑制剂的分类 通过物理方法鉴别可逆与不可逆的抑制作用
- 可逆抑制剂可以通过物理方法让酶恢复活力的抑制剂
  - 竞争抑制剂
    
    化学组成与构象同底物相似，能与酶结合，变相降低有效酶浓度
  - 非竞争抑制剂
    
    酶可以与（底物和抑制剂）【不分先后】同时结合形成三元复合物，但此复合物无法进一步反应
  - 反竞争抑制剂
    
    酶要先与底物结合，才能和抑制剂结合（多见于多底物反应）
- 不可逆抑制剂反之，一般通过共价键结合
  - 专一抑制剂
    
    专一地作用于某酶的活性部位的必需基团上
    K_cat型抑制剂也是酶的底物，在酶的催化下会使酶自己的基团失活
    K_s型抑制剂与底物结构类似，带有活泼化学基团，可修饰酶的活性基团
  - 非专一抑制剂
    
    作用在酶的一类或几类基团上
    有机磷：作用于丝氨酸的羟基
    有机汞/有机砷：作用于巯基
    重金属盐：高浓度失活，低浓度抑制
    烷化剂：使巯基、羟基、氨基、羧基等烷基化

抑制剂动力学 K_i 是抑制剂常数
- 竞争性抑制
  - $V = \frac{V_{max}[S]}{K_m (1 + \frac{[I]}{K_i})+ [S]}$
    双倒数式：
    $\frac{1}{V} = \frac{K_m}{K_{max}}(1 + \frac{[I]}{K_i}) \cdot \frac{1}{[S]} + \frac{1}{V_{max}}$
- 非竞争性抑制
  - $V = \frac{V_{max}[S]}{(K_m + [S])(1 + \frac{[I]}{K_i})}$
    双倒数式：
    $\frac{1}{V} = \frac{K_m}{K_{max}} (1 + \frac{[I]}{k_i})\frac{1}{[S]} + \frac{1}{V_{max}}(1 + \frac{[I]}{K_i})$
- 反竞争性抑制
  - $V = \frac{V_{max}[S]}{K_m + [S] \cdot (1 + \frac{[I]}{K_i})}$
    双倒数式：
    $\frac{1}{V} = \frac{K_m}{K_{max}} \frac{1}{[S]} + \frac{1}{V_{max}}(1 + \frac{[I]}{K_i})$

环境等因素对酶促反应的影响

温度温度系数Q_n：指每增加n℃，前后反应速率之比
pH 酶有最适pH，大多数酶的最适pH在5～8之间。（动物：6.8～8.0）（植物微生物：4.8～6.5）
原因：
- 过酸过碱影响空间构象
- 影响络合物解离
- 影响底物解离
- 影响有关基团解离
- 解离其他基团造成空间构象改变
激活剂 可以提高反应速率的物质
- 无机离子
- 小分子有机物
- 某些酶（激活酶原的激酶）

酶的作用机理及调节·

酶的活性部位
- 功能区域
  - 结合部位专一性
  - 催化部位催化反应性质
- 特点
  - 占比小
  - 三维实体
  - 不完全锲合（诱导）
  - 位于酶分子表面一个裂隙内
  - 结合底物靠较弱的次级键
  - 有一定的柔性与运动性

酶的基团
- 必需基团经过化学修饰后会使整个酶失活的基团
- 非必需基团修饰后不影响酶活性

研究活性部位的方法
- 酶侧链基团的化学修饰法
  鉴别修饰剂是否与酶的活性部位基团结合：
  - 酶活力丧失速率与修饰剂浓度正相关
  - 底物/与活性部位结合的可逆抑制剂可保护酶免受修饰剂的抑制
  修饰形式：
  - 非特异性共价修饰
  - 特异性共价修饰如DFP作用于胰凝乳蛋白酶Ser₁₉₅
  - 亲核标记
- 动力学参数测定法
- X射线晶体衍射法
- 定点诱变法
  
  一个个残基改变后测试

酶的催化机理·

影响酶催化效率的因素
- 邻近效应
  
  酶与底物间存在的亲和性会使之靠近，因此酶活性中心附近的底物浓度会增加
- 定向效应
  
  底物向酶的活性中心靠近时，会诱导酶的构象向底物反应基团与酶活性中心正确排列的方向转变
  酶的某些基团/离子会使底物敏感键中的基团的电子云密度向更敏感的状态去升高/降低。此时底物更接近过渡态。
酸碱催化

质子酸提供部分电子/质子碱接受部分电子以降低活化能。
酶中可作广义酸/碱的基团：Glu Asp Lys Arg Cys His Ser Tyr
共价催化

亲核/亲电子催化反应时分别放出/获得电子。作用于底物中心形成中间复合物降低活化能。（辅酶/辅基可参加（如：磷酰酶酰化酶葡糖酶））
亲核基团：His Cys Asp Ser 巯基羧基羟基咪唑基
亲电子基团：H⁺ Mg²⁺ Mn²⁺ Fe³⁺
金属离子催化

金属酶含紧密结合的金属离子
金属-激活酶含松散结合的金属离子
作用原理： 1.传递电子（许多氧化还原酶含Cu²⁺ Fe³⁺） 2.电荷屏蔽以促进反应（许多激酶底物为ATP-Mg²⁺复合物） 3.促进水的离子化以促进亲核催化
多元催化与协同效应

几个基元配合作用
如：胰凝乳蛋白酶Ser₁₉₅Asp₁₀₂His₅₇构成电荷中继网
活性部位的微环境

底物分子与酶活性部位结合，此时会形成疏水环境，因此，微环境极性降低，底物分子与酶活性部位间静电作用力增强。利于酶的催化反应。

酶的催化反应实例·

Lysozyme_溶菌酶切NAG_{氮乙酰氨基葡萄糖} 人们发现：

[s]（10^-4mol/L）相对水解率结构

(NAG)₂ 0 A-B

(NAG)₃ 1 A-B-C

(NAG)₄ 8 A-B-C-D

(NAG)₅ 4000 A-B-C-D-E

(NAG)₆ 30000 A-B-C-D-E-F

(NAG)₈ 30000 -

可得：

Lysozyme切割 D-E 间的键效率最高

在真实细胞壁中，NAG与NAM交替排列，因此：

Lysozyme作用于NAG-NAM-NAG-(NAM-NAG)-NAM

进一步：

Lysozyme 形如凹，中间的疏水裂缝恰好能容纳以上寡糖。
而Lysozyme发挥作用的氨基酸是Asp₅₂ Glu₃₅。
Glu₃₅上的质子转移到E环糖苷键上，使之断裂，此时，D环上的碳原子为C₂⁺，Asp₅₂上的O^-能暂时稳定C⁺，其后，OH^-与H₊分别与C₂⁺和Glu₃₅侧链结合，水解完成。

[s]（10^-4mol/L）	相对水解率	结构
(NAG)₂	0	A-B
(NAG)₃	1	A-B-C
(NAG)₄	8	A-B-C-D
(NAG)₅	4000	A-B-C-D-E
(NAG)₆	30000	A-B-C-D-E-F
(NAG)₈	30000	-

Ser蛋白酶_家族
- 胰蛋白酶 胰凝乳蛋白酶弹性蛋白酶
- 枯草杆菌蛋白酶凝血酶纤溶酶
- tPA 乙酰胆碱酯酶
以上三种酶虽然一级结构不太相似，但三维结构相似。
催化三连体：

His₅₇（酸碱催化担当） Asp₁₀₂（定位His₅₇） Ser₁₉₅（共价结合肽键使其断裂）
Ser羟基转移一个质子给His咪唑基上的N，使之带正电，可以与带负电的Asp静电稳定。此时，Ser羟基的O带负电，亲核攻击羰基上的C，形成共价化合物。（酰基酶）
其后，His₅₇N上的质子流向酰胺键上的N，形成不稳定化合物，发生肽键断裂，氨基产物释放。
再后，H₂0发动亲核攻击，OH 接原氨基酸的 C，H 接 His₅₇ Ser₁₉₅。于是，四面体瓦解，释放羧基产物。

核酸催化略（二轮复习再学）

酶活性的调节控制·

别构调节
- 概念多亚基酶分子的非催化部位与某些化合物非共价结合，使酶的构象发生变化，从而影响酶的活性。（别构酶/变构酶）
  使酶别构的物质为别构剂/效应物，一般是小分子代谢物/辅助因子
  正效应物/别构激活剂，负效应物/别构抑制剂
  酶上有和底物/调节物结合的部位，这两个部位可以在同一亚基或不同亚基上
  - 同促效应
    
    活性部位和调节部位相同
  - 异促效应
    
    活性部位和调节部位不同。但，可能相互影响产生协同效应如：天冬氨酸转氨甲酰酶
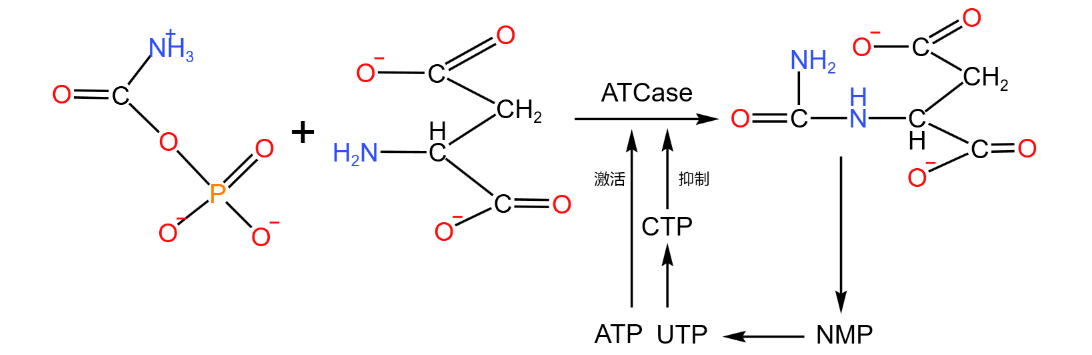
    ATCase 亚基排列 3R₂2C₃
- 酶促反应动力学不符合米氏方程
  
  [S]对V ，正协同 S形，负协同表观双曲线。
  对正协同来说 [S]对V求导，导数大
  对正协同来说 [S]对V求导，[S]在0附近的导数大，但随即导数下降到接近0 Kashland标准协同指数（CI）又饱和比数（RS）
  $\frac{ 结合位点饱和90%时[S] }{ 结合位点饱和10%时[S] } = 81^{ \frac{ 1 }{ n } }$
  其中，n为 Hill系数。n>1：正协同效应别构酶，n<1：负协同效应别构酶，n=1：米氏酶
- 调节机制
  - 齐变模型（MWC）对称亚基 -> 齐步变化 -> 对称亚基
    1. 别构酶是由确定数目亚基组成的寡聚酶，众亚基平等，有对称轴
    2. 每个亚基对一种调节物只有一个结合位点
    3. 每种亚基都有紧密构象与松弛构象
    4. 构象状态改变时对称性不变
  - 序变模型（KNF）全T -> 有T有R -> 全R
    1. 配体不存在时，酶的构象为T（紧密构象）
    2. 按序依次变化
    3. 亚基间可以是正/负协调作用

酶原激活 $\ce{ 酶原 ->[水解酶][不可逆] 酶 }$
胰蛋白酶原的转化：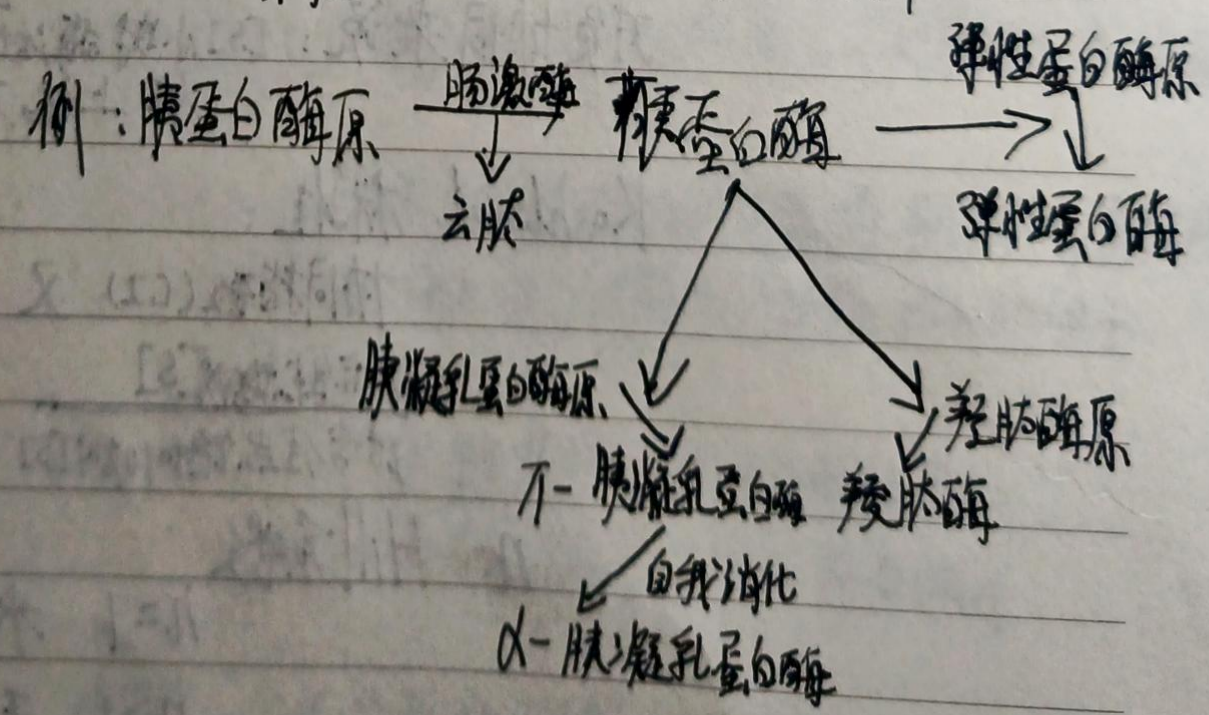
凝血机制

可逆共价修饰 共价修饰酶可通过其他酶共价修饰己身多肽链上的一些基团来调节活性
特点：
- 反应灵敏
- 节约能量
- 机制多样
- 常受激素/神经之指令
- 级联放大，高效快捷
例如：
- 磷酸化修饰（重点）
  - $\ce{ 蛋白质 <=>[ ATP -> ADP 蛋白激酶 ][ nPi <- H_2O 蛋白磷酸酶 ] 蛋白质-nP }$
  两类蛋白激酶：
  1. Ser/Thr羟基蛋白激酶
  2. Tyr羟基磷酸化蛋白激酶
  三类蛋白磷酸酶：
  1. Ser/Thr蛋白磷酸酶
  2. Tyr蛋白磷酸酶
  3. 两重底物型蛋白磷酸酶
  例如：
  蛋白激酶A的激活（cAMP依赖）（R₂C₂，每个R上有两个cAMP位点）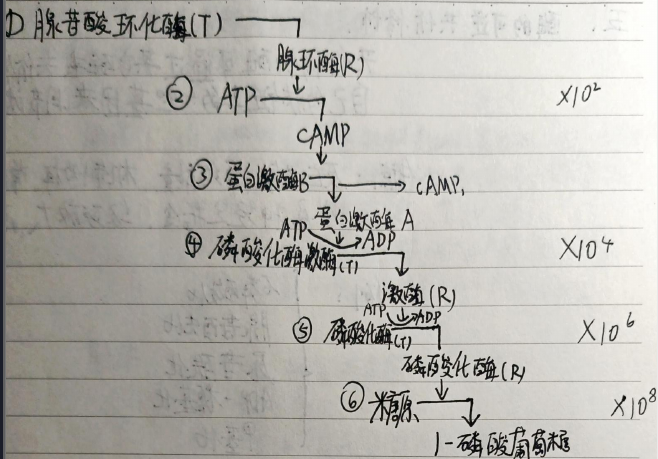
- 腺苷酰化修饰
- 尿苷酰化修饰
- ADP-糖基化修饰
- 甲基化修饰

同工酶isoenzyme 具有不同分子形式但催化相同化学反应的一组酶
意义：
- 遗传标志
- 和个体发育分化密切相关
- 适应不同代谢需求而产生的差异
例如：
1. 乳酸脱氢酶（LHD）由 4个 2种不同亚基组成。因此有 $ C^2_4 - 1 = 5 $ 种LHD，即H₄ ~ M₄。
  不同组织的细胞中LHD₁ ~ LHD₅ 含量不同。可诊断疾病。
2. 大肠杆菌中的天冬氨酸激酶的同工酶

考点总结及名词解释·

有待补充